半加算器をNANDとNORだけで構成する

半加算器(Half adder)というのはは、2つの1桁2進数に対する足し算を行い、和(Sum)と繰り上げ(Carry)を求める回路です。
今回は、半加算器の論理回路をNANDとNORだけで構成する方法について説明します。


まず、半加算器の振る舞いを押さえる為に、”NANDとNORだけ”という話は一旦おいといて、真理値表を確認します。

–半加算器の真理値表–

二入力のいづれか片方が1の場合は和(S)が1で、両方が1の場合は桁上げになるので繰り上げ(C)が1になります。

出力であるSとCのパターンに着目すると、一目瞭然でS(和)はXOR、キャリーはANDになっていることが分かります。
なので、もし任意の論理回路をを使ってもよければ、半加算器は以下の2素子で回路構成できます。






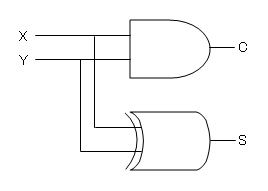
次に、上記の回路ををNANDとNORだけで作ってみます。
※なぜNANDとNORだけの回路に組み替えたいかというと、NAND,NORだと回路製造上で必要なトランジスタ数が少なくなり、コストメリットがある為です。


まず繰り上げ側(C)であるAND処理は簡単で、NANDを2つ用意すればOKです。

まず普通に2入力をNANDに入れて、その出力の否定を取ればANDが作れます。
NANDからNOTを作るには、二つの入力値を同一にすればOKです。




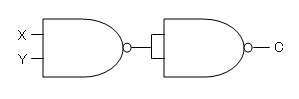
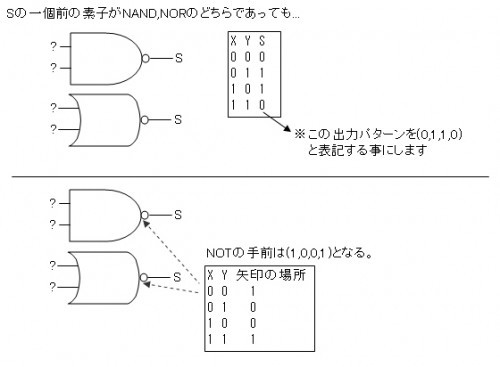
次にCのXOR(0,1,1,0の出力)はちょっと考え方に工夫が必要で、これはゴールから逆算したほうが分かりやすいです。
NAND,NORだけで作るという前提なので、Cの直前の素子がNAND,NORのどちらであったとしても、最後はNOTになります。
なのでNOTが入る直前の真理値は(1,0,0,1)です。






仮に、Cの手前の素子がNORだったと仮定した場合、(1,0,0,1)をorで作る事になるので、2つの入力は必ず(1,0,0,0)と(0,0,0,1)となります。

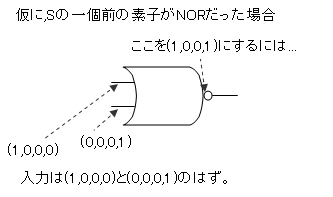
※OR回路だったら、他に(1,0,0,1)の入力も有りうるのでは?　と思われえるかもしれませんが、もし(1,0,0,1)を入力できるのであれば、それ自身が既に求めたい答えなので、後続のNOR回路はそもそも必要ありません。故に2つの入力は(1,0,0,0)と(0,0,0,1)の2つになります。



この内、(0,0,0,1)は先ほどCの出力と同じなので、こっちから引っ張ってこれます。

また、もう一方の入力である(1,0,0,0)は、よく見るとXとYのNORで作り出すことが出来ます。
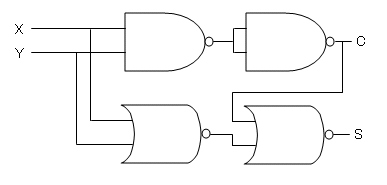
なので、半加算器をNAND,NORだけで構成させようとすると、以下の4素子で組み立てることが出来ます。